Ph.D in Astrophysics

Specialising in Stellar Magnetohydrodynamics.

I spent a fair few years engaged in part time research for a Ph.D in Astrophysics, specialising in Stellar Magnetohydrodynamics. This Ph.D was being undertaken under the supervision of Dr Gillian Pearce, an expert on Solar Sympathetic Flaring Phenomena and Supernovae.

The Ph.D involved developing flaring mechanisms by undertaking mathematical and computational modelling of the evolution of flares on stellar surfaces. A special area of interest was sympathetic flaring, where multiple flares erupt in close proximity to each other. I was working on the magnetic field containment for an evolving plasma such as that seen in a Solar Flare.

The computational side of the simulations, involved writing code first in C and C++, and then in Java, on SUN Workstations and on PC`s running Windows and Linux.

Gradually though, the combination of trying to run my company, help my partner who was ill throughout that time, alongside the Ph.D, took their toll, and I had to curtail the Ph.D since my partner needed a lot of support, and it was running the company that put food on the table, rather than the Ph.D.

Research.

How do you even start to model magnetohydrodynamics ? Well, whilst it would be a far greater undertaking than can be described in one solitary web page, there is a good place to start, and that is applying Maxwell's Equations to the model. Whilst it's hardly going to be helpful for a detailed analysis, here is the very, very start of development, the application of Maxwell's equations:

1) This equation demonstrates that either currents or time-variant electric fields generate magnetic fields. It is often referred to as Ampere’s Law.

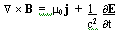
2) This equation shows the non-existence of magnetic monopoles, and from this the implication that a magnetic flux tube has a constant strength along its length.

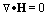
3) This equation is known as Faraday’s Law, and illustrates that time varying magnetic fields result in electric fields.

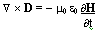
4) This equation is Gauss’s Law. Gauss’s Law shows that electric charges can generate electric fields.

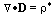
but since H = B / u₀ and D = e₀ E, the magnetic field and electric displacement can be eliminated to give :

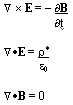
where;
E is the electric field (V m^-1 ),
j is the current density (A m^-2 )
p^* is the charge density,

u and e are approximated by their values in vacuum for the solar plasma case.

u = u₀ and e = e₀

where;
u₀ is the magnetic permeability (4 x pi x 10^-7 H m^-1 )
e₀ is the permittivity of free space (8.854 x 10^-12 F m^-1 )

such that c, the speed of light in a vacuum is given by ;

c = (u₀e₀)^-1/2 = 2.998 x 10⁸ m s^-1